How to share secrets? (Chinese version)

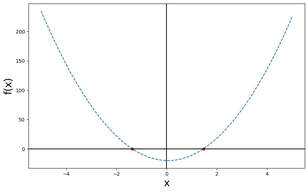
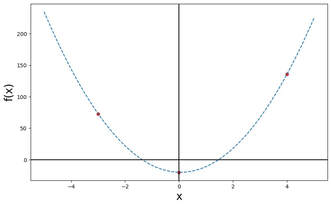
这篇博客我打算用中文写，其中一个原因是希望可以让更多的中国小朋友看懂而没有语言障碍。之前在中学的时候，相比于数学，我更喜欢的是物理学，其中一个原因就是我可以用想象来触碰和分析很多事情，比如采取一些质量无穷大这样的极限，总是可以带给我们一些感觉。而数学对我来说却感觉抽象的多。但是随着我听了更多人的数学课和看博客之后，我感觉我产生对于数学高冷的影响很多都是因为自己没有给自己产生很多例子，其实数学也是可以很有趣 ，很具象的。
这个博客想分享的一个事情是”如何分享秘密”。大概一个月前，我看到了一个博主在讲数学多项式的一些基本知识，我们在高中都学习过k阶多项式如果有(k+1)个点的信息，就可以唯一确定下来这个多项式的所有系数；反之，如果我们有的信息少于(k+1)个点，那么我们便没有可能复原这个多项式。就是这样一个简单的事情，我们可以拿它来做什么呢？接下来我们将会看到，即使是这样简单的高中数学知识，我们也可以拿它来做很酷炫的事情，比如设计一个“秘密的分享系统” (secrete sharing system)。
​首先，我们来复习一下什么是多项式，
\[f(x)=a_0+a_1*x + a_2*x^2+\cdots+a_k*x^k =\sum_{i=0}^{k}a_{i}*x^{i}\]
我们称f(x)为一个k阶多项式，其中\(a_0,a_1\cdots\)被称为这个多项式的系数。现在我们来看一个二阶多项式的例子：\(f(x)=-20-x+10x^2\)

那么上图就是这样一个二阶多项式的图像表示。这个函数每接受一个x的值，就会“吐出来”一个f(x)的值，这样你就有了很多很多(x,f(x))的点，他们组成了上面这条曲线。我们看到了上面有两个红色的点，我们称之为“零点”或者“根”。那我们还观察到了这个二阶多项式有两个根。一个自然的问题就是n阶多项式都有n个根嘛？不难证明以下定理:

• Theorem 1:在实数域\(\mathbb{R}\)上，如果一个n阶多项式有超过n个不同的根，那么它一定是零多项式，即多项式中所有的系数\(a_i\)都为0.

​所以我们看到一个n阶非零的多项式最多也就有n个零点。

那么假设我们提前不知道这个多项式的系数，而只知道它是一个三阶多项式，我们需要观测几个点才可以确定下来这个多项式呢？数学上有如下定理：

• Theorem 2:n阶多项式可以由(n+1)个不同的观测点(x,f(x))唯一确定下来

​也就是说，针对上图这种情况，如果我们已知是三阶多项式，我们需要四个红色的点就可以复原整条虚线了。但是如果我们观测的点少于四个，那么将会有无数条线都可以满足这个条件。那么利用这个性质，我们可以用它来做什么呢？我们可以用它来做一个密钥系统。

假设我们有一个秘密，这个秘密可以用数据D来表示，我们的目标是设计一个密钥系统把这个秘密D拆分成\(D_1,D_2,\cdots,D_n\),分给n个人，这个密钥系统可以实现：

• 当大于等于k个人提供出他们的\(D_i\)之后，系统可以解码秘密\(D\)
• 但是当少于k个人提供出他们的\(D_i\)之后，秘密\(D\)仍然是完全不能确定的

这样一个密钥系统称之为\((k,n)\)阈值方案。一个很经典的阈值方案在1979年被以色列科学家Adi Shamir提出（就是RSA加密里面的S先生）。这个方案就基于了上述的多项式的性质。假设我们的秘密可以被一个整数\(D\)来描述，我们选择一个大的质数\(p\),以下所有运算都是针对\(p\)的模运算。那么我们可以随机生成一个\(k-1\)阶的多项式：
\[q(x)=a_0+a_1*x+\cdots+a_{k-1}*x^{k-1}\]
使得\(a_0=D\)，然后我们可以计算\(D_1=q(1),D_2=q(2),\cdots,D_n=q(n)\)分配给n个人。这样任何超过\(k\)个\(D_i\)放在一起都可以解码\(D\)，而少于\(k\)个\(D_i\)都完全没法确定\(D\)，即\(D\)是在[0,p]之间等概率分布的。
这样一个密钥系统有什么好处呢？

• 首先，它可以根据人的层级来分配他拿到的部分信息的重要性。假设一个公司有一个总裁，和2个副总裁还有几个经理，这个公司的任何文件通过都需要4票通过，根据股权总裁具有三票投票权，副总裁具有两票投票权，经理具有一票投票权，总股权是n，那么我们可以设计一个这样的\((4,n)\)阈值方案，给总裁\(D_1,D_2,D_3\),副总裁\(D_4,D_5\)，以此类推。那么每次远程讨论某议题结束需要投票的时候，统一的人可以自动把自己的密钥\(D_i\)放到系统里面，如果有超过四个密钥被收集到，系统就会解码\(D\)，进而访问公司内部文件。如果没有四个密钥被收集，那么将不能解码，也就是投票失败。
• 其次，产生密钥信息\(D_i\)是dynamic的，所以当有新的人拿到投票权之后我们可以很容易产生新的\(D_i\)而不影响其他人，和系统的密码\(D\)，删除也是如此
• 并且，我们可以很容易的定期更新每个人手上的密钥\(D_i\)而无需修改密码\(D\)

​
​这篇文章的加密方案是1979年由Adi Shamir(著名RSA加密中是S-先生)提出的，这篇文章只有短短两页，运用的数学知识也是大家都学过的中学数学，却可以写出如此精妙绝伦的故事，让我看完之后时常感叹，也许这就是创造力吧！
疫情期间发生的事情千奇百怪，不过每次阅读到经典的论文，或者专注下来思考的时候，很多外部的扰动就消失了，能有时间坐下来完成一些有趣的事情，而不是为了达到某些目的而做事情，真的是一种奢侈的享受。